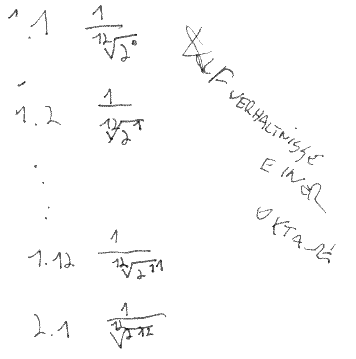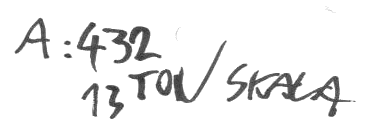phat
.
[GruftBox] - FreeScale/Frequenz und Skalen in Oszillatoren & P.ENV
FreeScale
Wer nicht weiß was die Gruftbox ist, und um was es hier geht > schaut bitte in das Allgemeine Thema zum Projekt: viewtopic.php?f=13&t=75682
Die Ergebnisse sollen in einer Groovebox oder einen Drumsynth eingesetzt werden, es geht also um schnell aber tiefgreifende Veränderungsmöglichkeiten, (so wenig wie möglich so viel wie nötig).
Es soll einfach und Livetauglich bleiben > genauer gesagt es geht um Elektronische-Live-Jam-Musik.
Und ich weiß das ist der spannendste Teil von allen, ich hab mich schon mit FreeScale Aufgabenstellung mit MaxMSP und Kopfhörer selbst VersuchsKaninchent, was Frequenzen anstellen können - ist einfach der Hammer
in diesem Zusammenahg, werden folgende Dinge hier diskutiert:
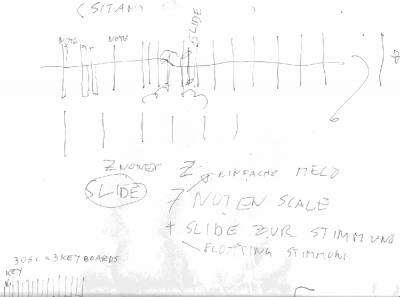
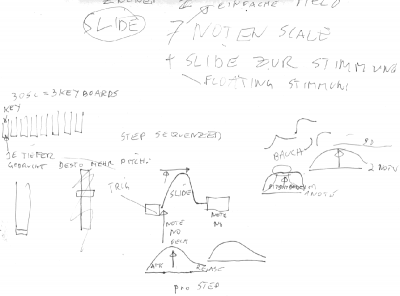
Portamento, Glide Was passiert zwischen den Tönen, wie können wir uns künstlerisch ausdrücken, den soul spielen - welche Geräte gibt es, und welche sollte es geben, wie sehen sie aus die Eingabegeräte für unsere JamSession, Plug and Rec & Play
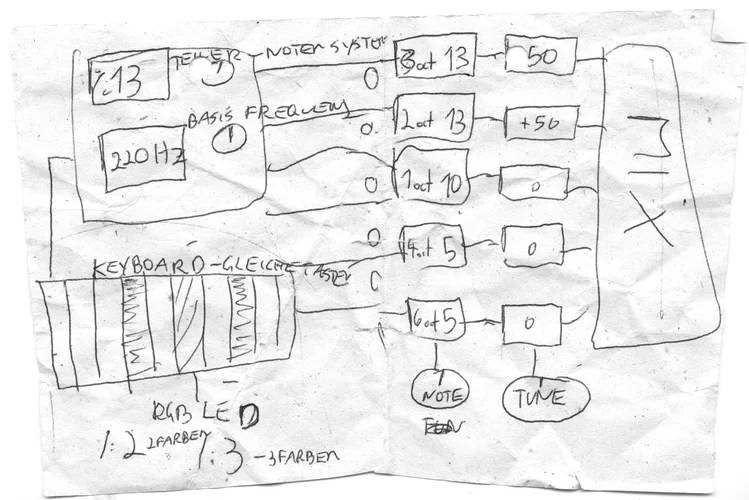
Grundrequenzen - kein Kammerton A mehr, hier wird frei eingestellt!
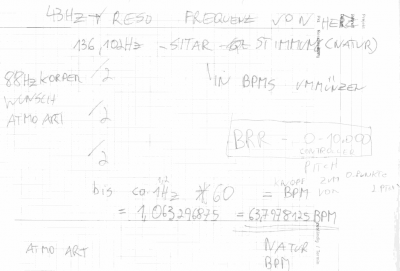
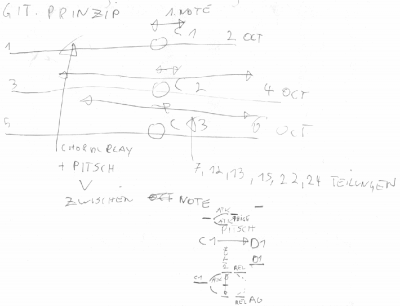
Oktavierung - Verdopplung der GrundFrequenz = erhöhung um 1 Oktave - hier wird so lange verdoppelt oder dividiert bis eine beliebige Frequenz hörbar ist, Reso-Freq. von Materie DNA, Schließmuskeln, Planeten, Farben Herzschlägen, Gehirnfrequenzen, Galaktischen Frequenzen, und was auch immer einen in den Kram passt - wird ab jetzt so lange transponiert bis es hörbar ist und dann arbeiten wir damit!
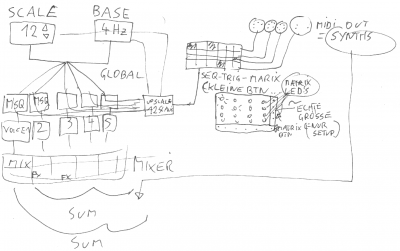
Skalierung- Teilung dieser Oktave > 12 in d.Klassik vorherschend, in der Groovebox der ZUKUNFT ist die Scale FREI einstellbar! - Harmonische 12?, ich kann das SCHWELLENDE Pulsierende wählen oder das "perfekte" wähle was du willst! Hauptsache die Grundfrequenz bleibt für das JAM-Setup gleich.
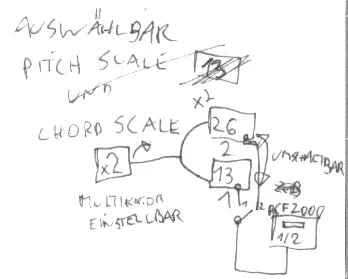
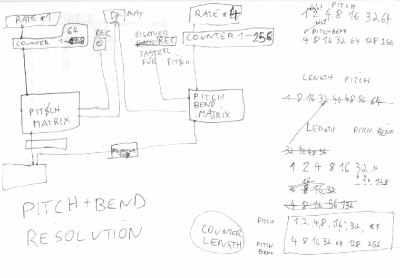
die Scale sollte durchgängig sein, so kann die NotenSkale 9 betragen, die feiner einstellbaren Chords der Oscillatoren sollten ein vielfaches dessen feiner sein - z.B. 18Scale, oder 36Scale.
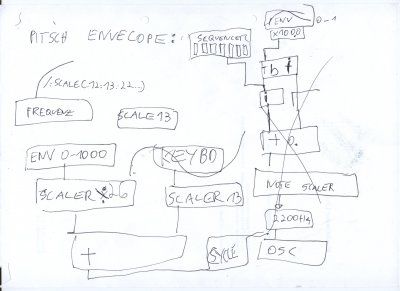
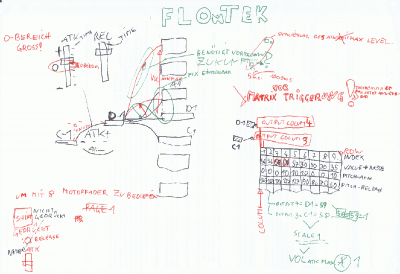
Das ganze damit Harmonisch - sollte (fein genug) auch in der Pitch-Envelope platz finden ----> es soll immer geil klingen - DAS IST MAL EIN WORT!
Die Skalierung ist nicht gleich die Dividierung in gleiche Teile, Gesetze wie der Goldene Schnitt, Greisfrequenz, sowie eigene Erfahrungen und Emotionen bestimmen die Teilung, manche Teile einer Skale werden gar ganz weggelassen, weil sie nie zu passen scheinen, doch ein Nie gibt es nicht, man sieht ein komplexes Thema.
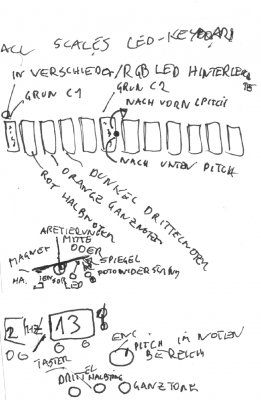
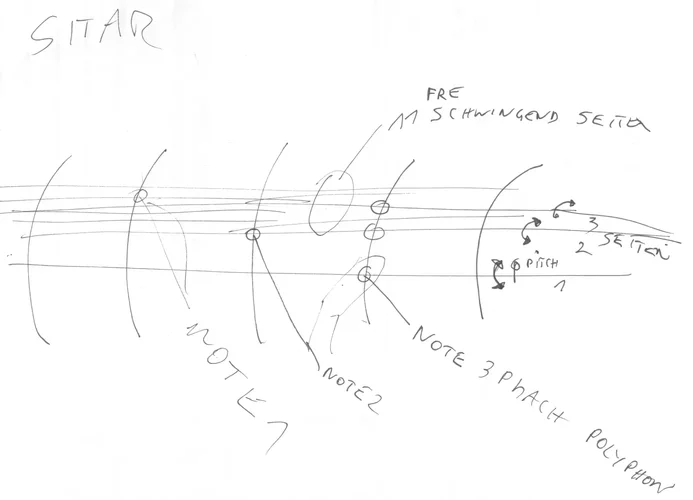
Eingabegeräte für Musik mit freier Skalenwahl es fängt bei schwarzen und weißen Tasten an, und endet ihrgendwo bei einer Hexagon RGB ButtonMatrix mit diversen Farben für Skalen unterteilungen...es geht zu String-Bend eingabegeräten mit simplen 6Skale skalierungen mit Pitcheingabe zur spielung der Noten dazwischen (ähnlich der indischen Sitar) > was der Groovebox und einer Envelope wieder näher liegt usw.....
Ich denke es gibt viel zu diskutieren, und am Ende sollte es so ausdiskutiert sein, das JEDER es checkt und keiner mehr Sagt > ich kenn mich mit Musik einfach nicht aus > ich hab das NIE gelehrnt und jeder ders nicht gelehrnt hat, hat den vorteil der kreativen Freiheit für neue instrumente- dafür brauch wir aber auch unlang länger
Allgemein:
> Userinterface: Userbility, Livetauglichkeit, schneller Zugriff, übersichtlichkeit, Reglergröße arangierung, Fader Drehregler Knöpfe µC gesteuerte Touchscreens usw.
> Baupläne für spezielle dafür ausgelegte Midi/OSC/USB-controller,
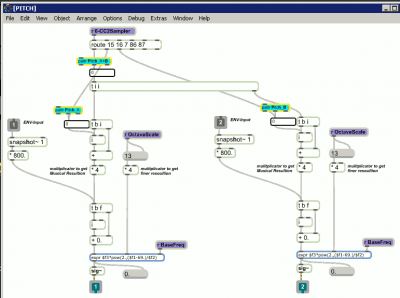
> Programmierung mittels MaxMSP, und Test auf Standart Midicontrollern (z.B. BCR2000)
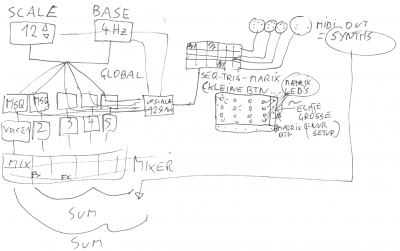
> Blockdiagramme
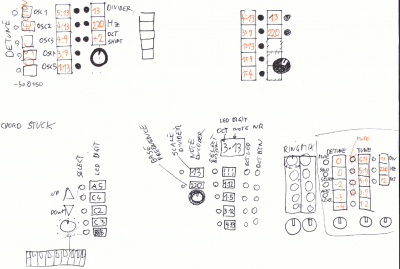
> Skizzen
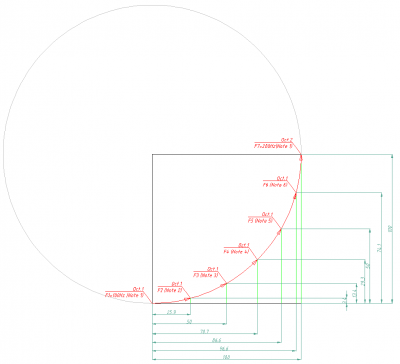
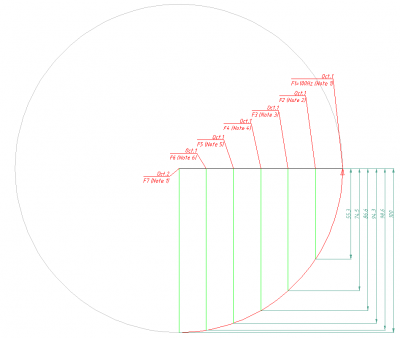
> CADzeichnungen
> Videos von Prototypen oder MaxMsp Tests
> sowie Soundtest usw
Ich freue mich auf die Diskussion sowie eure Erfahrungen mit diversen Skalen und Frequenzen und dessen Wirkungen,
Ganz ohne Mathematik gehts hier auch nicht - zumindest nicht was die Umsetzung in ein Programm angeht (ich hab da schon laufende Programme, doch dazu später, wenn Zeit), genau dieses Thema ist aber eines der Wichtigsten in einem Groovebox projekt, ich hatte schon etliche grooveboxen mit midicontrollern erstellt, von klein bis sündhaftteuer
Wenn es groß wird, dann wird es komplex, wird es komplex, hält man die Harmonie nicht, bzw sucht nach Ihr - eine Rasterung eine Skalierung - ist dann unabdingbar - wir reden ja bei einer Groovebox nicht von einem Instrument
das man perfekt beherscht, man bedient damit ein ganzes Orchester - wer Gott ist kann sich freuen, die anderen werden sich über vernünftige Skalierung freuen - denn der SOUL ist schwer zu finden!
SO - Ab gehts! WIRKT (ASO UND WIE IMMER IN DER GRUFTBOX - > NUR KAN STRESS!)
FreeScale
Wer nicht weiß was die Gruftbox ist, und um was es hier geht > schaut bitte in das Allgemeine Thema zum Projekt: viewtopic.php?f=13&t=75682
Die Ergebnisse sollen in einer Groovebox oder einen Drumsynth eingesetzt werden, es geht also um schnell aber tiefgreifende Veränderungsmöglichkeiten, (so wenig wie möglich so viel wie nötig).
Es soll einfach und Livetauglich bleiben > genauer gesagt es geht um Elektronische-Live-Jam-Musik.
Und ich weiß das ist der spannendste Teil von allen, ich hab mich schon mit FreeScale Aufgabenstellung mit MaxMSP und Kopfhörer selbst VersuchsKaninchent, was Frequenzen anstellen können - ist einfach der Hammer
in diesem Zusammenahg, werden folgende Dinge hier diskutiert:
Portamento, Glide Was passiert zwischen den Tönen, wie können wir uns künstlerisch ausdrücken, den soul spielen - welche Geräte gibt es, und welche sollte es geben, wie sehen sie aus die Eingabegeräte für unsere JamSession, Plug and Rec & Play
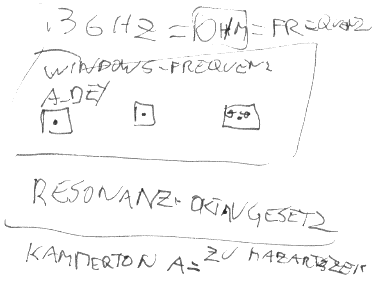
Grundrequenzen - kein Kammerton A mehr, hier wird frei eingestellt!
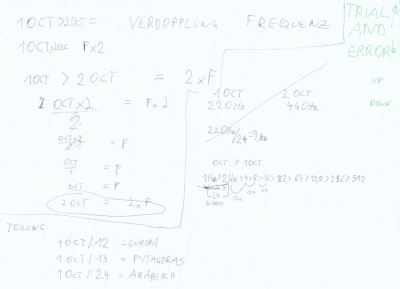
Oktavierung - Verdopplung der GrundFrequenz = erhöhung um 1 Oktave - hier wird so lange verdoppelt oder dividiert bis eine beliebige Frequenz hörbar ist, Reso-Freq. von Materie DNA, Schließmuskeln, Planeten, Farben Herzschlägen, Gehirnfrequenzen, Galaktischen Frequenzen, und was auch immer einen in den Kram passt - wird ab jetzt so lange transponiert bis es hörbar ist und dann arbeiten wir damit!
Skalierung- Teilung dieser Oktave > 12 in d.Klassik vorherschend, in der Groovebox der ZUKUNFT ist die Scale FREI einstellbar! - Harmonische 12?, ich kann das SCHWELLENDE Pulsierende wählen oder das "perfekte" wähle was du willst! Hauptsache die Grundfrequenz bleibt für das JAM-Setup gleich.
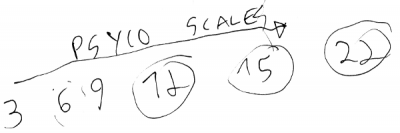
die Scale sollte durchgängig sein, so kann die NotenSkale 9 betragen, die feiner einstellbaren Chords der Oscillatoren sollten ein vielfaches dessen feiner sein - z.B. 18Scale, oder 36Scale.
Das ganze damit Harmonisch - sollte (fein genug) auch in der Pitch-Envelope platz finden ----> es soll immer geil klingen - DAS IST MAL EIN WORT!
Die Skalierung ist nicht gleich die Dividierung in gleiche Teile, Gesetze wie der Goldene Schnitt, Greisfrequenz, sowie eigene Erfahrungen und Emotionen bestimmen die Teilung, manche Teile einer Skale werden gar ganz weggelassen, weil sie nie zu passen scheinen, doch ein Nie gibt es nicht, man sieht ein komplexes Thema.
Eingabegeräte für Musik mit freier Skalenwahl es fängt bei schwarzen und weißen Tasten an, und endet ihrgendwo bei einer Hexagon RGB ButtonMatrix mit diversen Farben für Skalen unterteilungen...es geht zu String-Bend eingabegeräten mit simplen 6Skale skalierungen mit Pitcheingabe zur spielung der Noten dazwischen (ähnlich der indischen Sitar) > was der Groovebox und einer Envelope wieder näher liegt usw.....
Ich denke es gibt viel zu diskutieren, und am Ende sollte es so ausdiskutiert sein, das JEDER es checkt und keiner mehr Sagt > ich kenn mich mit Musik einfach nicht aus > ich hab das NIE gelehrnt und jeder ders nicht gelehrnt hat, hat den vorteil der kreativen Freiheit für neue instrumente- dafür brauch wir aber auch unlang länger
Allgemein:
> Userinterface: Userbility, Livetauglichkeit, schneller Zugriff, übersichtlichkeit, Reglergröße arangierung, Fader Drehregler Knöpfe µC gesteuerte Touchscreens usw.
> Baupläne für spezielle dafür ausgelegte Midi/OSC/USB-controller,
> Programmierung mittels MaxMSP, und Test auf Standart Midicontrollern (z.B. BCR2000)
> Blockdiagramme
> Skizzen
> CADzeichnungen
> Videos von Prototypen oder MaxMsp Tests
> sowie Soundtest usw
Ich freue mich auf die Diskussion sowie eure Erfahrungen mit diversen Skalen und Frequenzen und dessen Wirkungen,
Ganz ohne Mathematik gehts hier auch nicht - zumindest nicht was die Umsetzung in ein Programm angeht (ich hab da schon laufende Programme, doch dazu später, wenn Zeit), genau dieses Thema ist aber eines der Wichtigsten in einem Groovebox projekt, ich hatte schon etliche grooveboxen mit midicontrollern erstellt, von klein bis sündhaftteuer
Wenn es groß wird, dann wird es komplex, wird es komplex, hält man die Harmonie nicht, bzw sucht nach Ihr - eine Rasterung eine Skalierung - ist dann unabdingbar - wir reden ja bei einer Groovebox nicht von einem Instrument
das man perfekt beherscht, man bedient damit ein ganzes Orchester - wer Gott ist kann sich freuen, die anderen werden sich über vernünftige Skalierung freuen - denn der SOUL ist schwer zu finden!
SO - Ab gehts! WIRKT (ASO UND WIE IMMER IN DER GRUFTBOX - > NUR KAN STRESS!)