Rasenmähermann
||||||||||
Ich hab im netz gesucht, aber nichts gefunden, wie genau die envelopes vom juno 6/60 geformt sind. Wahrscheinlich sehen die vom 106er anders aus, oder sind komplett linear.
Jedenfalls hab ich ein vergleichsvideo gesehen zwischen dem deepmind 12 und dem juno 60.
Da wird übrigens dermaßen deutlich, wie wichtig envelopes und deren form sind.
Der juno 60 ist nicht umsonst so beliebt für sequenzen und arpeggios.
Gerade im Vergleich hört man wie der juno, den deepmind sowas von hinter sich lässt, wenn es um die hüllkurven bzw. deren Wirkung geht. Man kann das ja einstellen beim deepmind, aber anscheinend wurde das nicht gemacht, oder es geht nicht trotz verformung.
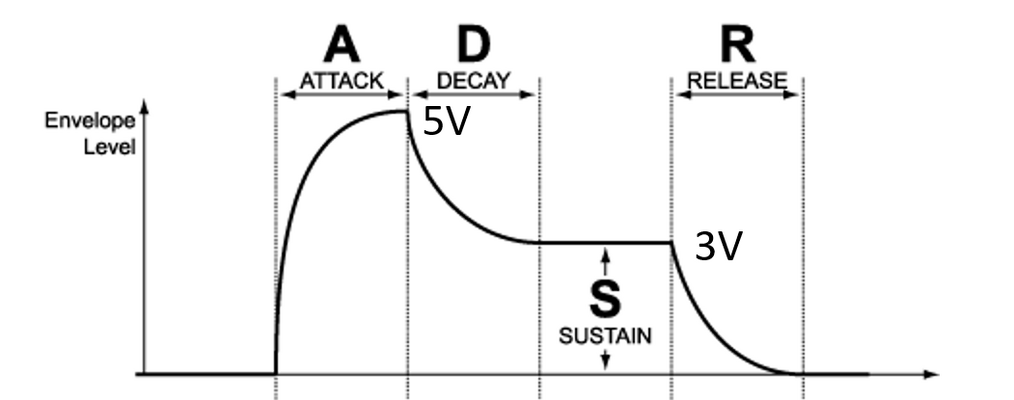
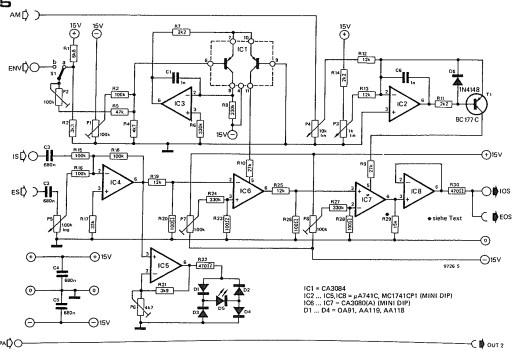
Der juno 60/6 hat ja analoge hüllkurven chips.
Gibt es ein bild von deren form?
Wie sind attack, decay und release geformt?
Ich erinnere mich, mal irgendwo gelesen zu haben, dass die envelopes komplett linear sind?
Welche hüllkurven gefallen euch am besten, bzw. von welchem synthesizer.
Und wie wichtig sind euch die hüllkurven generell? Zum beispiel beim Neukauf.
P. S..:
Ich denke, dass jede Komponente bei einem synthesizer wichtig ist. Hüllkurven und lfo's wurden lange nur stiefmütterlich behandelt. Schnell oder langsam?
Die form von lfo's und envelopes sind zwar nicht direkt klanggebend, aber trotzdem haben sie einen großen Einfluss auf diesen, besonders beim filter.
Wie sweetspotig ein synthesizer ist und für was er sich am besten eignet, wird dadurch mitbestimmt.
Juno und prophet 5 sind gute beispiele für Synergie. Alle komponenten beeinflilussen sich gegenseitig positiv.
Man kann ja auch bei manchen synth, die envelopes mit sich selbst modulieren.
Beim pro 3 find ich die hüllkurven wirklich nicht gut und die modulation ist dermaßen grob, dass ich sie gerade so ok hinbiegen kann, für die meisten fälle. Längere zeiten gehen so sehr gut, aber knackige sachen, kurze zeiten, sequenzen, pluckiges, wofür man den pro3 eigentlich nutzen will, klingt nicht sehr zufriedenstellend. Da scheint es also auch nochmal unterschiede zu geben, wie sie geformt sind. Also exponentiell ist nicht gleich exponentiell? Ich werde beim pro 3 mal andere hüllkurven nutzen und mir das mal anschauen, sobald ich zeit habe.
Außerdem frage ich mich inwiefern der vca und dessen summierung am schluss klangebend ist. Dafür interessiert sich auch fast keiner und ich habe mich selbst gar nicht damit beschäftigt. Da wollte ich auch mal rumprobieren, ob man irgendwelche unterschiede hören kann. Semimodular sei dank.
Jedenfalls hab ich ein vergleichsvideo gesehen zwischen dem deepmind 12 und dem juno 60.
Da wird übrigens dermaßen deutlich, wie wichtig envelopes und deren form sind.
Der juno 60 ist nicht umsonst so beliebt für sequenzen und arpeggios.
Gerade im Vergleich hört man wie der juno, den deepmind sowas von hinter sich lässt, wenn es um die hüllkurven bzw. deren Wirkung geht. Man kann das ja einstellen beim deepmind, aber anscheinend wurde das nicht gemacht, oder es geht nicht trotz verformung.
Der juno 60/6 hat ja analoge hüllkurven chips.
Gibt es ein bild von deren form?
Wie sind attack, decay und release geformt?
Ich erinnere mich, mal irgendwo gelesen zu haben, dass die envelopes komplett linear sind?
Welche hüllkurven gefallen euch am besten, bzw. von welchem synthesizer.
Und wie wichtig sind euch die hüllkurven generell? Zum beispiel beim Neukauf.
P. S..:
Ich denke, dass jede Komponente bei einem synthesizer wichtig ist. Hüllkurven und lfo's wurden lange nur stiefmütterlich behandelt. Schnell oder langsam?
Die form von lfo's und envelopes sind zwar nicht direkt klanggebend, aber trotzdem haben sie einen großen Einfluss auf diesen, besonders beim filter.
Wie sweetspotig ein synthesizer ist und für was er sich am besten eignet, wird dadurch mitbestimmt.
Juno und prophet 5 sind gute beispiele für Synergie. Alle komponenten beeinflilussen sich gegenseitig positiv.
Man kann ja auch bei manchen synth, die envelopes mit sich selbst modulieren.
Beim pro 3 find ich die hüllkurven wirklich nicht gut und die modulation ist dermaßen grob, dass ich sie gerade so ok hinbiegen kann, für die meisten fälle. Längere zeiten gehen so sehr gut, aber knackige sachen, kurze zeiten, sequenzen, pluckiges, wofür man den pro3 eigentlich nutzen will, klingt nicht sehr zufriedenstellend. Da scheint es also auch nochmal unterschiede zu geben, wie sie geformt sind. Also exponentiell ist nicht gleich exponentiell? Ich werde beim pro 3 mal andere hüllkurven nutzen und mir das mal anschauen, sobald ich zeit habe.
Außerdem frage ich mich inwiefern der vca und dessen summierung am schluss klangebend ist. Dafür interessiert sich auch fast keiner und ich habe mich selbst gar nicht damit beschäftigt. Da wollte ich auch mal rumprobieren, ob man irgendwelche unterschiede hören kann. Semimodular sei dank.