Du verwendest einen veralteten Browser. Es ist möglich, dass diese oder andere Websites nicht korrekt angezeigt werden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Du solltest ein Upgrade durchführen oder einen alternativen Browser verwenden.
Fakten Supercritical Redshift 6, analoger Desktopsynth mit "demon core" und MPE
- Ersteller microbug
- Erstellt am
Bitte ausschließlich klare belegte Fakten zum Thema, kein Blabla, keine Witze, Meinungen, sondern Daten und Fakten.
Moogulator
Admin
Das ist deren Entwicklung - und der Klang ist ja wirklich fantastisch, sowas kann man anderen Firmen anbieten, aber einfach so übernehmen wird man es sicher nicht können, ist ja auch nicht klar wie sie es genau tun. Denke aber, dass die Begrenzungen bezüglich Modulation schon schwere Nachteile sind - weil - ohne Sync, FM, etc - ist das schon mehr nur schön ,aber nicht immer auch ausreichend, aber das könnte nur mich betreffen, ich denke lange nach bevor ich etwas kaufe, was nicht anders schon geht mit dem was da ist.
Die anderen arbeiten anders, einige kommen auch auf sehr gute Wege, muss man sagen, zudem die technischen Ideen auch wilder sind heute und vielfältig auch.
Wie auch immer - ich finde den Redshift cool, ich würde sehr am f festhalten damit alles klappt und was man hört ist wirklich sehr schön, aber man muss auf jeden Fall noch was für Modulation der OSCs tun, …
Die anderen arbeiten anders, einige kommen auch auf sehr gute Wege, muss man sagen, zudem die technischen Ideen auch wilder sind heute und vielfältig auch.
Wie auch immer - ich finde den Redshift cool, ich würde sehr am f festhalten damit alles klappt und was man hört ist wirklich sehr schön, aber man muss auf jeden Fall noch was für Modulation der OSCs tun, …
swissdoc
back on duty
Magst Du Deine Vermutung mit uns teilen?Wenn man mal etwas darüber nachdenkt, dann ist es ziemlich klar, wie der "Demon Core Oscillator" im Redshift funktionieren muss.
swissdoc
back on duty
Muss man das? Müssen die Supercritical-Guys das?Wie auch immer - ich finde den Redshift cool, ich würde sehr am f festhalten damit alles klappt und was man hört ist wirklich sehr schön, aber man muss auf jeden Fall noch was für Modulation der OSCs tun, …
Danic
Don't Panic
Das MPE & Arp-Update ist jetzt verfügbar:
 supercriticalsynthesizers.com
supercriticalsynthesizers.com
Redshift 6 Firmware Update 1.4 | Supercritical Synthesizers
 supercriticalsynthesizers.com
supercriticalsynthesizers.com
Ja kann ich machen.Magst Du Deine Vermutung mit uns teilen?
Also wie kann man einen mächtigen digital kontrollierten analogen Oszillator realisieren, der ein 16-stimmiges Signal erzeugen kann (mehrere gegeneinander verstimmte Unisono-Stimmen oder auch Akkorde) wie beim "Demon Core Oscillator" im Redshift 6?
Eine naive Umsetzung durch 16 getrennte physische DCOs schließe ich aus, weil das zu viel Rauschen mit sich bringen würde.
Die Umsetzung als ein einzelnen Oszillator ist aber jetzt auch kein Dämonenwerk.
Gehen wir davon aus, dass der Oszillator die Grundwellenformen Dreieck, Sägezahn und Rechteck (mit einstellbarem Tastverhältnis) beherrschen soll und dass er im Prinzip beliebig viele Stimmen gleichzeitig erzeugen können soll.
Was bedeutet das in technischer Hinsicht?
Betrachten wir hierzu zuerst den Fall der Dreiecksschwingung.
Hier eine einzelne Dreiecksschwingung über 4 Perioden:
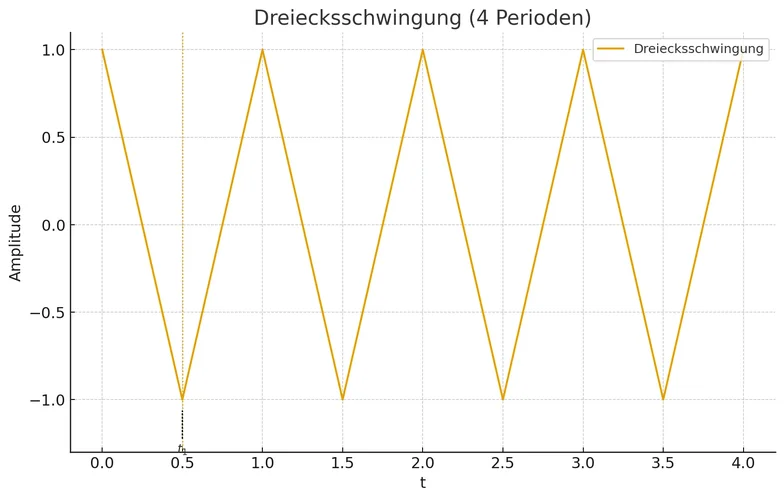
Für einen Unisono-Effekt würde man mehrere Dreiecksschwingungen kombinieren, die leicht gegeneinander verstimmt sind und in der Phase auseinanderlaufen, so wie hier gezeigt:
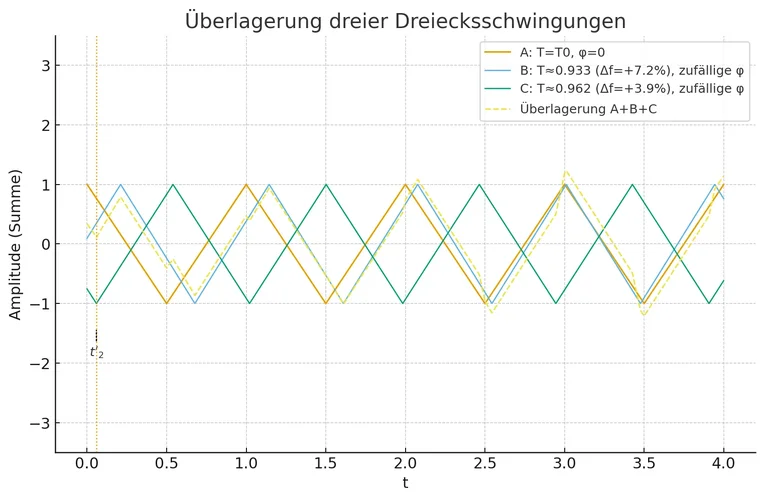
Addiert man die Signale, so erhält man diese Wellenform:
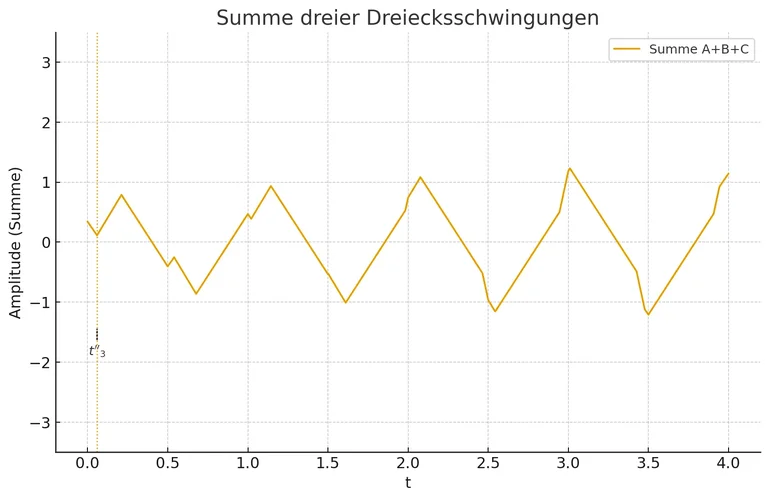
Jetzt ein wenig Mathematik: Die Dreieckswellenform ist ein Beispiel für eine stückweise lineare Funktion, sie besteht also aus einer Aneinanderreihung von Liniensegmenten.
Außerdem ist die Funktion stetig, d.h. der Verlauf erfolgt nahtlos und ohne Sprünge im Signalverlauf von Knickpunkt zu Knickpunkt.
Der Witz ist nun, dass die Summe von stückweise linearen Funktionen wieder eine stückweise lineare Funktion ist.
Das sieht man in der Grafik zur Summe der drei gegeneinander verstimmten Dreiecksschwingungen sehr gut.
Ein digital gesteuerter analoger Oszillator, der einen Mix (eine Summe) aus beliebig vielen Dreiecks-Wellenformen auf einmal erzeugen können soll, muss also lediglich in der Lage sein, beliebige stückweise lineare Signalverläufe zu erzeugen.
Mit welcher Steigung das gerade zu erzeugende Linien-Segment dann verlaufen soll und wie lange das Segment dauert, das muss in Software vorberechnet werden.
Wie das geht, kann man an dem Beispiel auch gut erläutern.
Angenommen, der letzte berücksichtigte Knickpunkt bzw. Kontrollpunkt lag bei t=0. Die Software kennt dann den Zielwert (y0 = Summe aller Signale) zu diesem Zeitpunkt.
Zur Ermittlung des nächsten zu generierenden Linien-Segments muss nun dessen Endzeitpunkt und y-Wert berechnet werden.
Für das zeitliche Ende des Segmentstücks wird einfach für jede der überlagerten Dreiecksschwingungen der Zeitpunkt des nächsten Knicks ermittelt. Der kleinste Wert hiervon ist der Endzeitpunkt das zu erzeugenden Segments (d.h. der erste Zeitpunkt, zu dem sich am aktuellen Linienverlauf etwas ändert).
In der mittleren Grafik ist dieser Zeitpunkt als t'_2 gekennzeichnet. Er entspricht dem ersten Knickzeitpunkt in der dritten Grafik mit der Summe (t''_3).
Nach Ermittlung des Summensignals bei t''_3 kennt man auch den y-Wert des nächsten Knickpunkts.
Daraus ergibt sich die Zeitdauer des aktuell zu erzeugenden Segments und seine Steigung (Differenz der y-Werte von aktuellem und letztem Stützpunkt, geteilt durch die Zeitdauer).
So hangelt man sich immer vom letzten Knickpunkt zum nächsten Stützpunkt durch und berechnet nach und nach alle Kontrollwerte für die Erzeugung des stückweise linearen Signalverlaufs.
Hier nun eine Skizze (Blockschaltbild), wie der eigentliche Oszillator aussehen könnte:
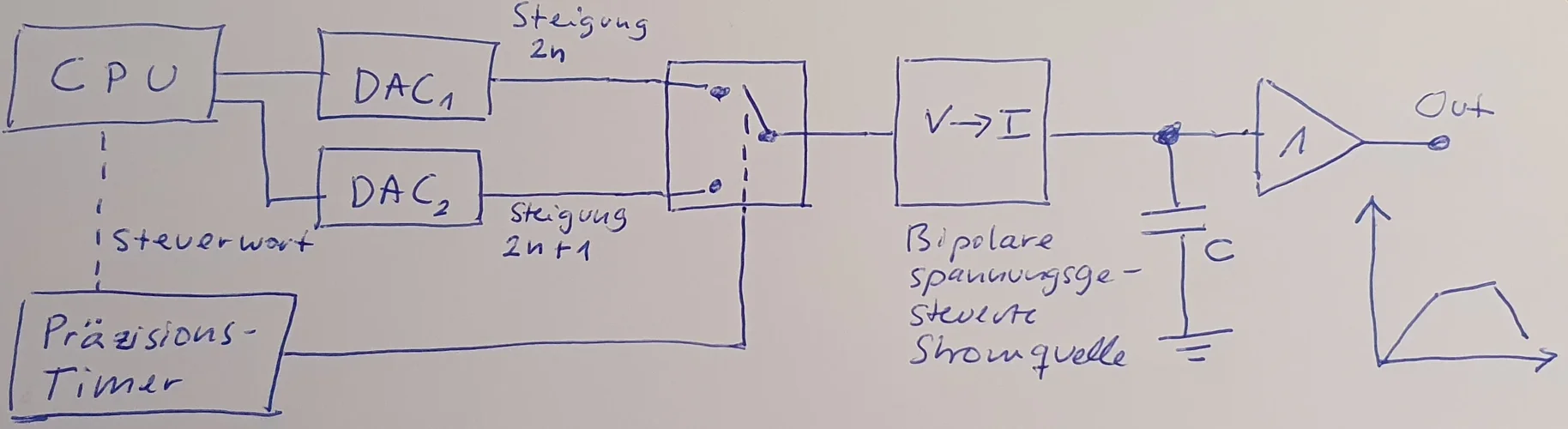
"CPU" steht für die digitale Steuerung, wie oben beschrieben. Es gibt zwei Digital-Analog-Wandler (DAC1 und DAC2), die die Steigung des aktuellen Liniensegments und die Steigung des nachfolgenden Liniensegments ausgeben. Die Steigungen werden abwechselnd von DAC1 (gerader Segment-Index) und DAC2 (ungerader Segment-Index) ausgegeben und in entsprechende Spannungen gewandelt.
Die Dauer des aktuellen Segments wird an einen Präzisions-Timer gegeben (das ist im Prinzip ein Zähler mit einer durch einen Quarz stabilisierten hohen Taktfrequenz). Nach Ablauf der Dauer des aktuellen Liniensegments schaltet dieser vom Ausgang des DACs für die aktuelle Steigung des Segments auf den Ausgang des DACs für die Steigung des nächsten Liniensegments um. Dies geschieht über einen 2:1 Analogschalter.
Am Ausgang des Analogschalters liegt somit eine Spannung, die proportional zur Steigung des zu generierenden Segments ist.
Der nächste Schritt ist eine spannungsgesteuerte Stromquelle, die sowohl positive als auch negative Ströme erzeugen kann (z.B. ein OTA / Operational Transconductance Amplifier). Die spannungsgesteuerte Stromquelle erzeugt nun einen Strom, der proportional zur Steigung des gerade zu erzeugenden Liniensegments ist.
Dieser Strom lädt einen Kondensator C auf (positive Ströme) bzw. entlädt ihn (negative Ströme). Dies geschieht linear, d.h. man erhält das gewünschte Linienstück im Signalverlauf mit der gewünschten Steigung.
Die Spannung am Kondensator wird über einen Impedanzwandler abgegriffen und als Ausgangssignal des Oszillators bereitgestellt.
Verallgemeinern wir dies nun auf den Fall der Sägezahn- und Rechteck-Wellenformen.
Hier ein einzelner Sägezahn:
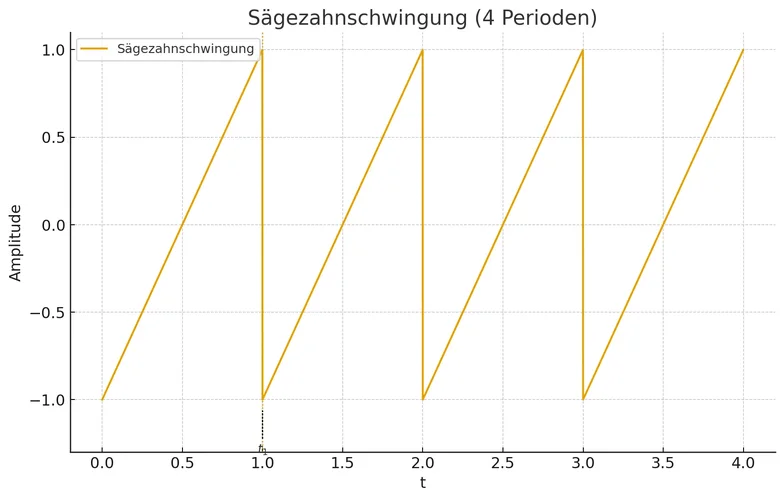
Hier eine Überlagerung von 3 Sägezähnen:
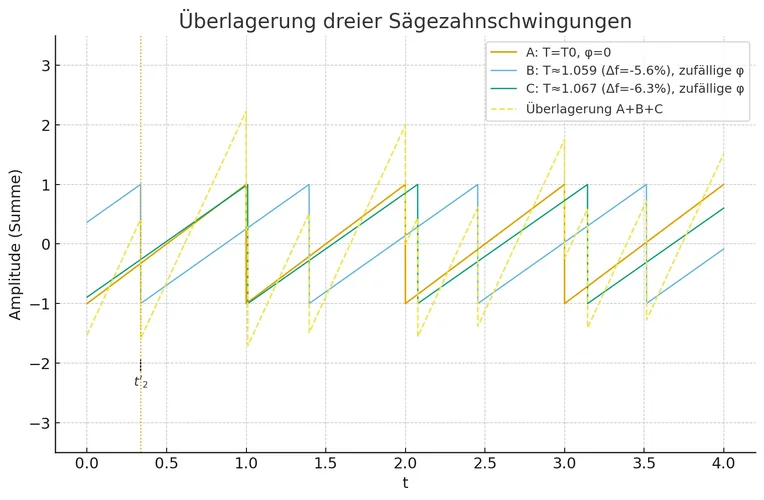
Hier das Summensignal, das erzeugt werden soll:
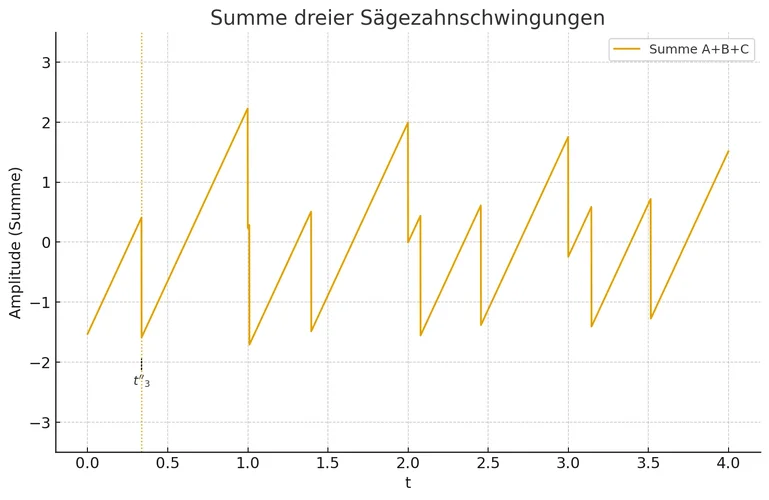
Im Unterschied zur Dreiecks-Wellenform haben wir hier eine stückweise lineare Funktion mit Sprungstellen. (D.h. die Funktion ist nicht stetig und springt an manchen Stellen zu einem neuen Wert).
Auch hier gilt aber: Die Summe von stückweise linearen Funktionen mit Sprungstellen ist wieder eine stückweise lineare Funktion mit Sprungstellen. Man muss also den Oszillator (und die Vorberechnung der Segmentdauern und -steigungen) nur so verallgemeinern, dass auch Wertsprünge korrekt berücksichtigt werden.
An der Berechnung der Zeitdauern ändert sich nichts.
Statt eines einzelnen einzelnen Knickpunkts haben wir nun aber beim nächsten Zeitpunkt, an dem sich der Linienverlauf ändert (t'_2 bzw. t''_3 in den Graphiken) zwei Kontrollpunkte: Den y-Wert für das Ende des aktuellen Segments und den y-Wert für den Start das darauf folgenden Liniensegments. Nennen wir diese y_e und y_s.
Für die Erzeugung des Signalverlaufs "mit Sprüngen" verdoppeln wir einfach den bisherigen Aufbau des Oszillators.
Der erste Oszillator hat die Aufgabe, das Liniensegment 1, 3, 5 usw. korrekt zu generieren.
Der zweite Oszillator hat die Aufgabe, das Liniensegment 2, 4, 6 usw. korrekt zu generieren.
Zwischen den Ausgangssignalen der Oszillatoren wird an jeder Sprungstelle mit einem 2:1 Analogschalter umgeschaltet.
Während der erste Oszillator das aktuelle Liniensegment i von y_s(i) zu y_e(i) generiert und dessen Endwert y_e linear ansteuert, kann der zweite Oszillator (während er gemuted ist) von seinem letzten Wert y_e(i-1) aus bereits linear den Startwert y_s(i+1) des Nachfolgesegments i+1 ansteuern. So hat er bereits den richtigen Startwert für das nächste Segment, wenn der Analogschalter beim nächsten Segment auf ihn umschaltet und sein Signal ausgibt.
Dasselbe Prinzip funktioniert auch bei Rechteck-Wellenformen.
Hier eine einzelne Rechteckwelle:
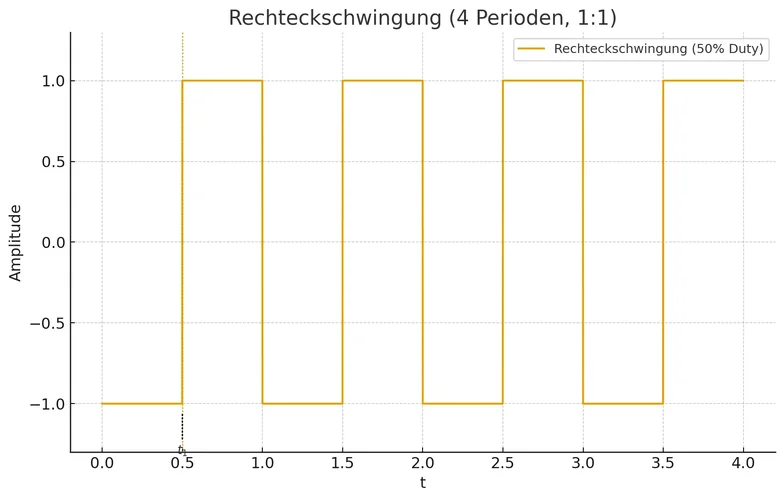
Hier 3 phasenverschobene und gegeneinander verstimmte Varianten:
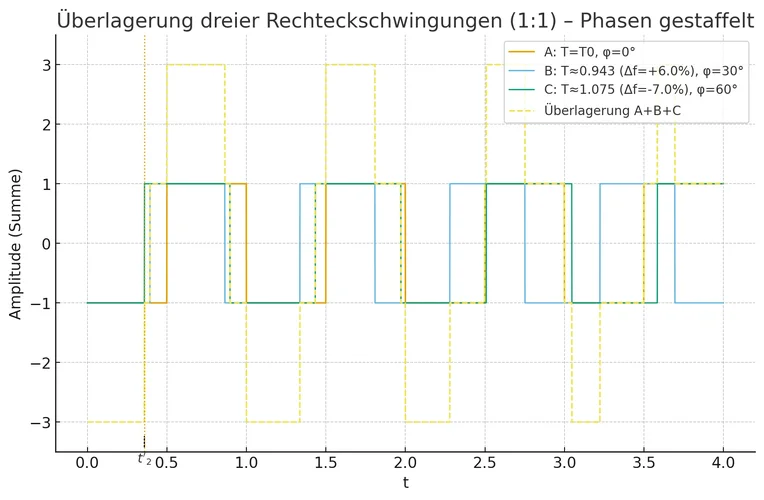
Hier die Summe der drei Einzelsignale:
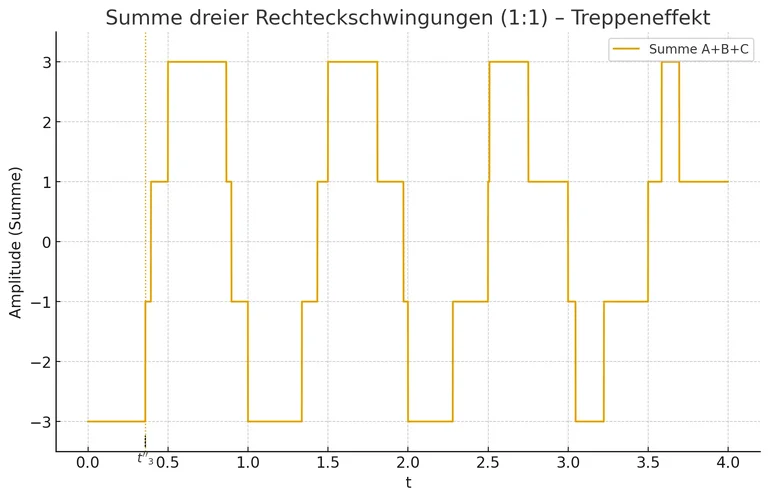
Auch hier ergibt sich eine stückweise lineare Funktion mit Sprungstellen. (Die Treppenfunktion ist ein Spezialfall davon, sie hat nur Sprünge und Stellen mit Steigung 0).
Ich hoffe, dass deutlich geworden ist, wie man einen Oszillator wie den Demon Core Oszillator realisieren könnte.
Ob er tatsächlich so realisiert ist oder ganz anders, weiß ich natürlich nicht.
Ein paar Schwierigkeiten sollten nicht verschwiegen werden:
- Es gibt zwei Taktraten, die des DAC (typische Sampling-Rate) und die des Präzisions-Timers (hohe Taktfrequenz im MHz-Bereich).
Sollten mehrere Kontrollpunkte in einen Sampling-Zeitraum des DAC fallen, so können sie nicht alle exakt bedient werden. Im Fall einer solchen "Kollision" muss aus den verschiedenen Kontrollpunkten innerhalb des betroffenen Sampling-Intervalls ein einzelner kombinierter Kontrollpunkt erzeugt werden (z.B. Durchschnitt der Dauern als Zeit-Dauer und Durchschnitt der y-Werte als Basis für die Ermittlung der Steigung).
Die Wahrscheinlichkeit einer solchen Kollision ist niedrig, aber sie steigt mit der Zahl der von dem Oszillator zu rendernden Stimmen. - Die spannungsgesteuerte Stromquelle wird in der Realität einen Offset haben (bei Steigung 0 nicht exakt den Strom 0 liefern) und könnte dadurch den Kondensator in eine Richtung immer weiter aufladen. Umgekehrt wird der Kondensator nicht die Spannung perfekt "halten", sondern sich durch Leckströme langsam gegen 0 entladen. Diese Effekte müssen in der Schaltung und in der Berechnung der Steuerwerte berücksichtigt werden.
- In der Praxis gibt es (durch Quantisierung) eine Beschränkung auf die darstellbaren Steigungen und auch eine maximal mögliche Steigung. Bei der Ermittlung der Steigungen für das nächste Segment ist als Startpunkt immer der Wert zu nehmen, die der Oszillator nach Anwendung dieser Beschränkungen auf die Parameter tatsächlich erreicht hat. Für den Zielpunkt dagegen sind jeweils die idealen, exakten Vorgabewerte zu nehmen.
Nach etwas Nachdenken würde ich Oszillator für den Fall von Sprungstellen (= Sägezahn, Rechteck) doch etwas anders aufbauen. OSC1 wird gebaut wie bei Dreieck. Er erzeugt eine stetige stückweise definierte lineare Funktion, indem er jeweils Liniensegmente von y_s(i) zu y_s(i+1) generiert.
Im Vergleich zum Zielsignal fehlt dann immer noch ein kleines Sägezahn-Stück, d.h. ein Liniensegment von 0 (beim Startzeitpunkt t_i des Segments) zu y_e(i) - y_s(i+1). Dieses lässt sich durch einen klassischen DCO realisieren, bei dem ausgehend vom Startpunkt 0 eine Steigung (positiv oder negativ) eingestellt wird und der Kondensator zum Zeitpunkt des Segment-Wechsels wieder schlagartig auf 0 entladen wird.
Die Ausgangssignale der beiden Oszillatoren werden addiert.
Dieser Ansatz sollte praktikabler sein als der ursprünglich beschriebene.
Hier noch ein Prinzipschaltbild für den verbesserten Ansatz:
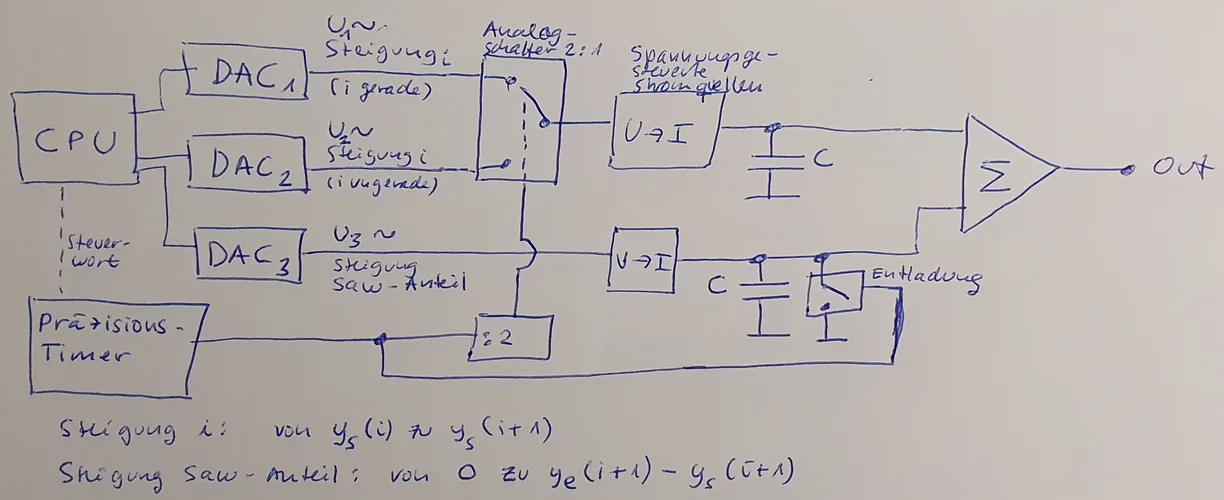
Zuletzt bearbeitet:
swissdoc
back on duty
@Turing
Wow, das ist ja fast ein Paper geworden. Vielen Dank. Ich hatte mir das vom Prinzip her genauso überlegt, ohne die vielen Details und die Vermutung mit einem befreundeten Synthesizerentwickler auf der SB25 geteilt. Er meinte nur trocken, wo dann der Unterschied zu einer komplett digital erzeugten Schwingungsform wäre. Ich habe das damals nicht weiter beantwortet. Der Vorteil ist einfach, dass man nicht bandlimitiert sein muss, es gibt keine Sample-Rate und zwischen den Stützstellen keine Quantisierung. Allerdings hat man wie bei einem konventionellen DCO eine Quantisierung der Frequenz. Da kann man allerdings Dithern, was bei den Stützstellen auch möglich wäre. FM und Sync müssten auch gehen, bei FM müsste man stückweise linear interpolieren und bekommt sicher hässliche Artefakte ins Signal.
Wow, das ist ja fast ein Paper geworden. Vielen Dank. Ich hatte mir das vom Prinzip her genauso überlegt, ohne die vielen Details und die Vermutung mit einem befreundeten Synthesizerentwickler auf der SB25 geteilt. Er meinte nur trocken, wo dann der Unterschied zu einer komplett digital erzeugten Schwingungsform wäre. Ich habe das damals nicht weiter beantwortet. Der Vorteil ist einfach, dass man nicht bandlimitiert sein muss, es gibt keine Sample-Rate und zwischen den Stützstellen keine Quantisierung. Allerdings hat man wie bei einem konventionellen DCO eine Quantisierung der Frequenz. Da kann man allerdings Dithern, was bei den Stützstellen auch möglich wäre. FM und Sync müssten auch gehen, bei FM müsste man stückweise linear interpolieren und bekommt sicher hässliche Artefakte ins Signal.
Die fehlende Bandlimitierung und die Aliasing-Freiheit sehe ich auch als den Hauptvorteil.
Die Quantisierung der Frequenz durch den Präzision-Timer ist so fein, dass sie keine praktische Rolle spielen sollte.
(In einem typischen DCO wie dem des Juno ist die Taktfrequenz z.B. 4 MHz. Damit wird eine Genauigkeit bei der Umsetzung der "Knickpunkte" von 0.000000125 Sekunden erreicht, wenn man für den Präzisions-Timer immer zum nächstgelegenen Rasterpunkt bzgl. der Taktfequenz rundet).
Bei FM und Sync sehe ich erst einmal ein "Paarungsproblem": Welcher der n Stimmen, die Oszillator A generieren kann, soll welche der m Stimmen von Oszillator B syncen bzw. in der Frequenz modulieren?
Bei FM kommt dann noch als Problem dazu, dass das exakte Ergebnis nicht mehr linear ist und dass man, wie Du ja schon schreibst, interpolieren müsste.
Dasselbe gilt auch für Ringmodulation, bei dieser entstehen Signalverläufe mit quadratischen Anteilen.
Die Quantisierung der Frequenz durch den Präzision-Timer ist so fein, dass sie keine praktische Rolle spielen sollte.
(In einem typischen DCO wie dem des Juno ist die Taktfrequenz z.B. 4 MHz. Damit wird eine Genauigkeit bei der Umsetzung der "Knickpunkte" von 0.000000125 Sekunden erreicht, wenn man für den Präzisions-Timer immer zum nächstgelegenen Rasterpunkt bzgl. der Taktfequenz rundet).
Bei FM und Sync sehe ich erst einmal ein "Paarungsproblem": Welcher der n Stimmen, die Oszillator A generieren kann, soll welche der m Stimmen von Oszillator B syncen bzw. in der Frequenz modulieren?
Bei FM kommt dann noch als Problem dazu, dass das exakte Ergebnis nicht mehr linear ist und dass man, wie Du ja schon schreibst, interpolieren müsste.
Dasselbe gilt auch für Ringmodulation, bei dieser entstehen Signalverläufe mit quadratischen Anteilen.
Zuletzt bearbeitet:
Sie könnten statt statischem Detuning der Unisono-Stimmen auch einen Ensemble-Oszillator realisieren, bei dem n Stimmen jeweils ein Vibrato mit einer Phasenverschiebung von 360° / n erhalten (ähnlich zum klassischen Ensemble-Effekt mit n=3).
Ich weiß nicht, ob der Redshift so etwas schon kann, aber es würde sich evtl. besser oder zumindest anders anhören als die typischen Multi-Unisono-Klänge, also mehr in Richtung Stringer.
Ich weiß nicht, ob der Redshift so etwas schon kann, aber es würde sich evtl. besser oder zumindest anders anhören als die typischen Multi-Unisono-Klänge, also mehr in Richtung Stringer.
Es könnte eine spezielle Engine für FM, Sync und Ringmodulation geben, mit ganz anderem Konzept.
Interessant: auf dem Kanban Board mit der Roadmap ist so einiges entfernt worden:
Kein Pole-Mixing Filter mehr und so Sachen. Merkwürdig. Sehr merkwürdig.
Im SC Discord hat jemand etwas ähnliches gefragt (Features von der Roadmap verschwunden) und hat eine Antwort erhalten:
traffkin — 02.10.25, 06:21
i seem to be missing something... where're all those brave tasks in the roadmap, like new osc models etc? abandoned or just postponed?
Viiri — 02.10.25, 07:34
Neither of those. We’re just planning to replace the current roadmap with something else after the 1.6 update.
swissdoc
back on duty
Neue Roadmap nun hier einsehbar:
 supercriticalsynthesizers.com
supercriticalsynthesizers.com
Cool, dass jetzt für November die FXs anstehen.
Redshift 6 | Supercritical Synthesizers
 supercriticalsynthesizers.com
supercriticalsynthesizers.com
Cool, dass jetzt für November die FXs anstehen.
swissdoc
back on duty
Ich warte sehnlichst auf das Pole Mixing Filter, das hatten sie auf der SB24 schon gezeigt und es war nicht klar, dass es gar nicht im Initial Release sein würde.Cool, dass jetzt für November die FXs anstehen.
mioo
∞
Ähnliche Themen
- Antworten
- 2
- Aufrufe
- 1K
News
-
News Sounddesign und Auswahl - Studiomöbel und Aufstellung - 2 Themen im SequencerTalk 261 - live 20:30
- Gestartet von Moogulator
- Antworten: 1
-
News Multitimbral - Wie viele unterschiedliche Stimmen bietet dein Synthesizer - SequencerTalk 260
- Gestartet von Moogulator
- Antworten: 2
-
-
News Morbid Angstpop Song-Herausforderung 2026 - Abgabe 1.2.2026 - SeqSquad Song Battle
- Gestartet von Moogulator
- Antworten: 0
-
-
-
Browser Split View - Zwei Sites auf einmal ansehen & vergleichen
- Gestartet von Moogulator
- Antworten: 2
App installieren
So wird die App in iOS installiert
Folge dem Video um zu sehen, wie unsere Website als Web-App auf dem Startbildschirm installiert werden kann.
Anmerkung: Diese Funktion ist in einigen Browsern möglicherweise nicht verfügbar.